Interactive Shape Deformation
Interactive deformation is an important aspect of geometry processing, used for instance in CAGD and the movie industry. In our work, shape manipulation is driven by a variational optimization, which guarantees high quality deformations by minimizing physically-inspired energies subject to user-controlled constraints (Figures 1,2). We distinguish between linear and nonlinear approaches, depending on whether the energy minimization leads to the solution of a linear or nonlinear problem.


Minimizing quadratic approximations of deformation energies leads to a linear system to be solved for the deformed surface each time the user changes the constraints or drags some surface points. These so-called multiple right-hand side problems can be solved efficiently using sparse Cholesky factorization (Botsch et al., 2005). Precomputing deformation response functions, which can then be evaluated instead of solving the linear system, even allows for real-time mesh editing (Botsch & Kobbelt, 2004).
Space deformations warp the whole embedding space of an object, instead of computing the deformation on the surface mesh only. As a consequence, the complexity and stability of the deformation is decoupled from the object’s mesh representation, such that on the one hand very complex models, and on the other hand also point clouds or irregular triangle soups can be processed. In (Botsch & Kobbelt, 2005) we represent the space deformation by triharmonic radial basis functions, which provides smoothness guarantees similar to surface-based deformations. Since each mesh vertex is now transformed individually, the involved computations can be delegated to the programmable shaders of recent graphics hardware, which enables real-time shape editing of complex models at a rate of 30M vertices/sec (Figure 3).

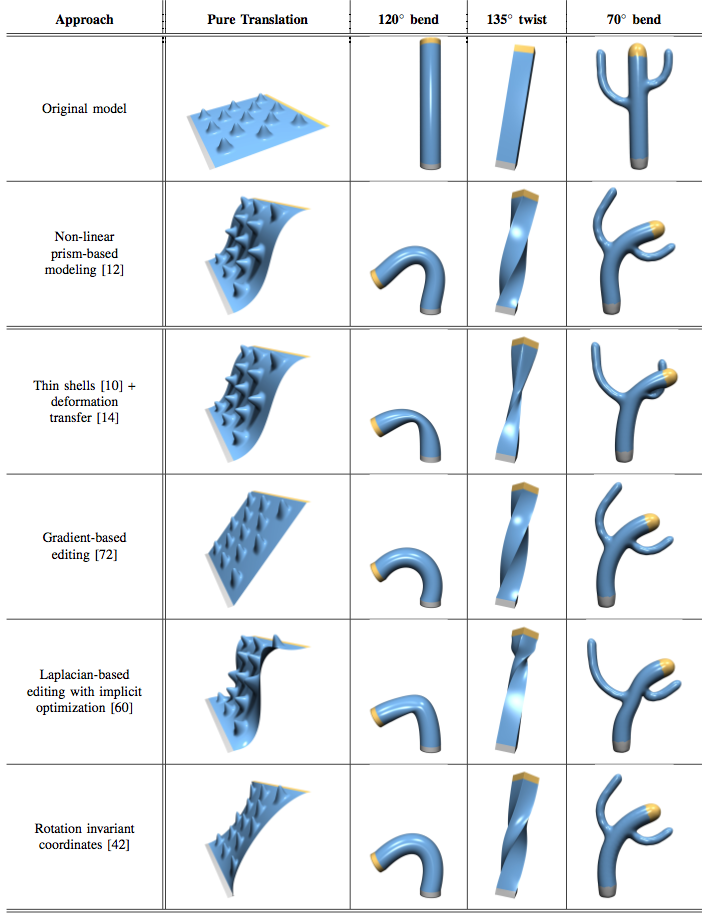
While linear deformation approaches are extremely efficient, the involved linearizations can lead to artifacts under large deformations, in particular for large rotations (Figure 4), as we analyzed in our survey (Botsch & Sorkine, 2008). In such cases, nonlinear deformation techniques have to be employed. However, since then a nonlinear constrained minimization problem is to be solved for each step of an interactive deformation, particular attention has to be paid to computational efficiency and numerical robustness.
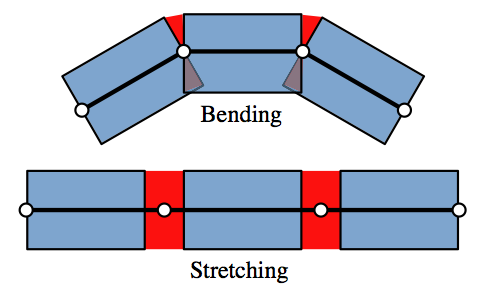
In (Botsch et al., 2006) we developed a new nonlinear method for 3D surface deformation that achieves intuitive and robust deformations by emulating physically plausible surface behavior inspired by thin shells. The surface mesh is embedded in a layer of volumetric rigid cells, which are coupled through non-linear, elastic forces (Figure 5). To deform the mesh, cells are rigidly transformed to satisfy user constraints while minimizing the nonlinear elastic energy. The nonlinearity allows for intuitive results even under large scale deformations. The rigidity of the prisms prevents degeneration even under extreme deformations, making the method numerically stable. Our modeling framework allows for the specification of various geometrically intuitive parameters that provide control over the physical surface behavior (Figure 6).

Interactive performance is achieved by a hierarchical multi-grid solver (Botsch et al., 2006) or by an adaptive space deformation approach (Botsch et al., 2007). For the latter, the object is embedded into an adaptively refined octree-like voxelization (Figure 7), which can even be dynamically refinement during object deformation (Figure 8).