Discrete Laplacians for General Polygonal and Polyhedral Meshes

Astrid Bunge

TU Dortmund

Marc Alexa

TU Berlin

Mario Botsch

TU Dortmund

🚀 by Decker

Slides are available online

http://graphics.rocks/polygons

Problem Setting

Solve PDEs on surface meshes and volume meshes

images/vw.png Surface mesh images/bunny-tets.png Volume mesh

Laplacian is a central operator

Gradient (direction of steepest ascent) \[ \grad f(u,v) \;=\; \vector{ \pdiff{f}{u} \\ \pdiff{f}{v} } \]
Divergence (magnitude of source or sink) \[ \func{div}\of{\vec{f}(u,v)} \;=\; \func{div} \vector{f_1(u,v) \\ f_2(u,v)} \;=\; \pdiff{f_1}{u} + \pdiff{f_2}{v} \]
Laplace (difference to average of local neighborhood) \[ \laplace f(u,v) \;=\; \func{div} \grad f \;=\; \frac{\partial^2 f}{\partial u^2} + \frac{\partial^2 f}{\partial v^2} \]

Diffusion Equation: $\dot f = \lambda \laplace f$

Laplace Equation: $-\laplace f = 0$

Discrete Laplacian has various applications

Mean Curvature
Smoothing & Fairing
Parameterization
Deformation
Geodesics Distances
…

images/swiss-army-knife.png — Find their presentation here

Discrete Laplacians for Polygonal/Polyhedral Meshes

images/vw.png Surface Meshes: ~~Triangles~~ Polygons images/bunny-tets.png Volume Meshes: ~~Tetrahedra~~ Polyhedra

Artist-Made Polygon Meshes

Cutting & Fracturing

Cutting Simulation

Discrete Laplacians for Polygonal Meshes

images/vw.png Surface Meshes: ~~Triangles~~ Polygons images/bunny-tets.png Volume Meshes: ~~Tetrahedra~~ Polyhedra

Triangulate the Polygons?

Outline

Introduction
Laplacian for Triangle Meshes
Laplacian for Polygon Meshes
- Martin et al., Polyhedral finite elements using harmonic basis functions, SGP 2008
- Alexa & Wardetzky, Discrete Laplacians on general polygonal meshes, SIG 2011
- de Goes et al., Discrete differential operators on polygonal meshes, SIG 2020
- Bunge et al., Polygon Laplacian made simple, EG 2020
- Bunge et al., The Diamond Laplace for polygonal and polyhedral meshes, SGP 2021
- Bunge et al., Variational quadratic shape functions for polygons and polyhedra, SIG 2022
Comparisons & Conclusion

Triangle Meshes

Connectivity / Topology
- Vertices $\mathcal{V} = \{ v_1, \dots, v_n \}$
- Edges $\mathcal{E} = \{ e_1, \dots, e_k \}$, $e_i \in \mathcal{V} \times \mathcal{V}$
- Faces $\mathcal{F} = \{ f_1, \dots, f_m \}$, $f_i \in \mathcal{V} \times \mathcal{V} \times \mathcal{V}$

Geometry
- Vertex positions $\{ \vec{x}_1, \dots, \vec{x}_n \}$, $\vec{x}_i \in \R^3$

Functions on Triangle Meshes

Define a piecewise linear function on a triangle mesh as \[f(\vec{x}) = \sum_{i \in \set{V}} f_i \varphi_i(\vec{x})\]
- Assign function values $f_i$ to vertices $v_i$ with positions $\vec{x}_i$
- Assign linear “hat” basis functions $\varphi_i(\vec{x})$ to vertices $v_i$
- Equivalent to barycentric interpolation of $f_i$ within triangles

Barycentric Coordinates as Shape Functions

Piecewise linear functions
Interpolate nodal data: $\varphi_i\of{\vec{x}_j} = \delta_{ij}$
Partition of unity: $\sum_i \varphi_i\of{\vec{x}} = 1$
Barycentric property: $\sum_i \varphi_i\of{\vec{x}} \vec{x}_i = \vec{x}$
$C^0$ across elements, $C^1$ within elements

Laplace Matrix & Mass Matrix

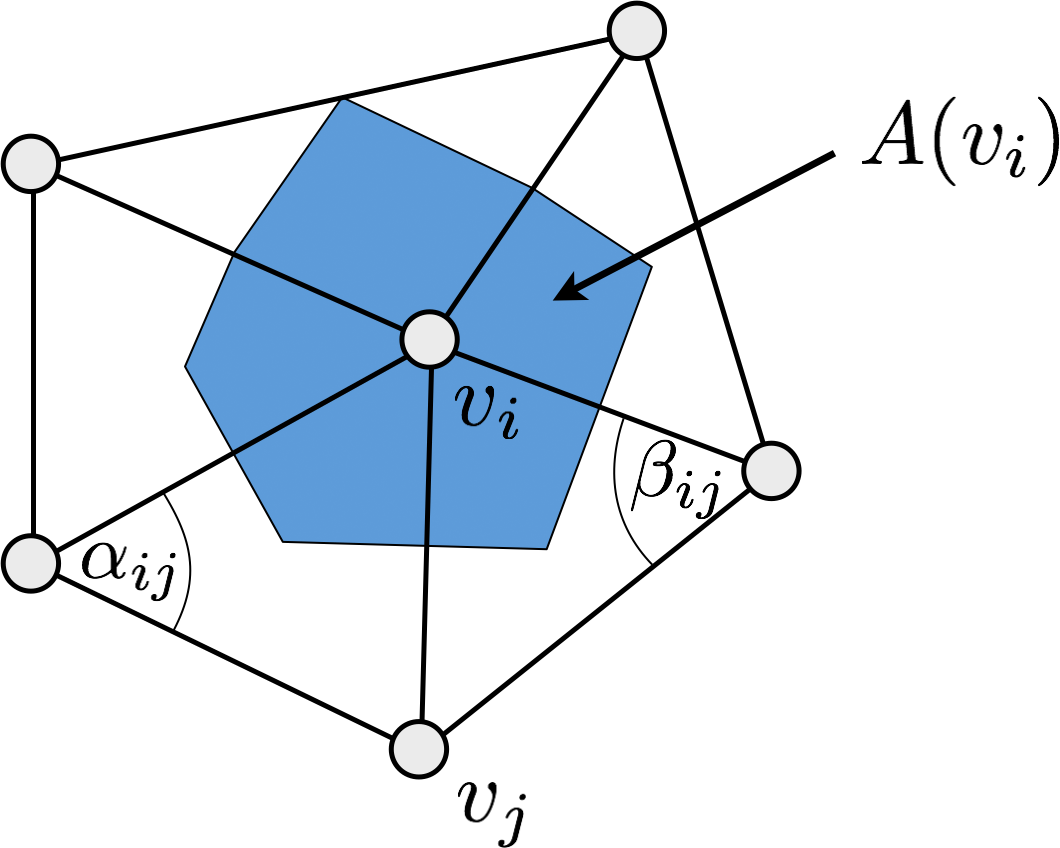
\[ \small \begin{eqnarray*} \mat{L}_{ij} &=& -\int \grad \varphi_i \cdot \grad \varphi_j &=& \begin{cases} \frac{\cot\alpha_{ij}+\cot\beta_{ij}}{2} & \text{if } j\in\set{N}\of{i} \,, \\[0.5em] \displaystyle -\sum_{k\in\set{N}\of{i}} \mat{L}_{ik} & \text{if } j=i \,, \\[0.3em] 0 & \text{otherwise}. \end{cases} \\[1em] \mat{M}_{ij} &=& \int \varphi_i \, \varphi_j &=& \begin{cases} \frac{\abs{t_{ijk}} + \abs{t_{jih}}}{12} & \text{if } j\in\set{N}\of{i}\,, \\[0.5em] \displaystyle \sum_{k\in\set{N}\of{i}} \mat{M}_{ik} & \text{if }j=i \,,\\[0.3em] 0 & \text{otherwise}. \end{cases} \end{eqnarray*} \]

Local to Global Assembly

images/local_Lf.svg images/global_L.svg

Properties

Symmetry
- Continuous Laplacian is selfadjoint
Locality
- Laplacian of a function $u$ at point $\vec{x}$ should only depend on small neighborhood
Linear precision
- Laplacian of linear functions should be zero on planar regions

Negative semi-definiteness
- Ensures that Dirichlet energy does not switch signs
Null property
- Kernel of the Laplacian should only contain constant functions
Positive weights
- Sufficient condition for maximum principle

continous L has a set of key properties that discrete L must able emulate
correlation (for triangles) discussed by Wardetzky et al., equally holds for polygons.
Symmetry: contionus L selfadjoint, and every selfadjoint operator is symmetric, so discrete L should be a symmetric matrix.
Locality: The L of a function u at a point x should only depend on other points in an small epsilon environement around that point.
Linear Precision: on planar regions, the L of linear functions should be zero. So, the discrete equivalent should also hold for planar meshes.
NSD/PSD: dirichlet energy, (can be expressed with the help of S), remains greater equal zero.
null Property: kernel should be 1D -> only constant functions.
Positive weights: sufficent, but not necessary for the maximum principle.
solutions of diffusion problem flow from higher potnentials to lower ones.
not all props are always satisfied on all meshes!

Properties

Poisson System on 2D Triangle Meshes

images/triangle_plane1.png images/triangle_plane2.png images/triangle_plane3.png images/triangle_plane4.png images/triangle_plane5.png

Poisson System on 2D Triangle Meshes

7.28224, 14.5124, 28.9698, 57.8831, 115.709
Cotan Laplacian, 0.0184139, 0.00457148, 0.00115444, 0.000291485, 7.33316E-05
<!--
{
  "options": {
    "scales": {
      "x": {
        "title": {
          "text": "inverse mean edge length",
          "display": true
        }
      },
      "y": { 
        "title": {
          "text": "L2 error",
          "display": true
        }
      }
    }
  }
}
-->

Poisson System on 2D Triangle Meshes

7.28224, 14.5124, 28.9698, 57.8831, 115.709
Cotan Laplacian, 0.0184139, 0.00457148, 0.00115444, 0.000291485, 7.33316E-05
<!--
{
  "options": {
    "scales": {
      "x": {
        "title": {
          "text": "inverse mean edge length",
          "display": true
        },
        "type": "logarithmic"
      },
      "y": { 
        "title": {
          "text": "L2 error",
          "display": true
        },
        "type": "logarithmic"
      }
    }
  }
}
-->

Outline

Introduction
Laplacian for Triangle Meshes
Laplacian for Polygon Meshes
- Martin et al., Polyhedral finite elements using harmonic basis functions, SGP 2008
- Alexa & Wardetzky, Discrete Laplacians on general polygonal meshes, SIG 2011
- de Goes et al., Discrete differential operators on polygonal meshes, SIG 2020
- Bunge et al., Polygon Laplacian made simple, EG 2020
- Bunge et al., The Diamond Laplace for polygonal and polyhedral meshes, SGP 2021
- Bunge et al., Variational quadratic shape functions for polygons and polyhedra, SIG 2022
Comparisons & Conclusion

Barycentric Coordinates

Piecewise linear functions
Interpolate nodal data: $\varphi_i\of{\vec{x}_j} = \delta_{ij}$
Partition of unity: $\sum_i \varphi_i\of{\vec{x}} = 1$
Barycentric property: $\sum_i \varphi_i\of{\vec{x}} \vec{x}_i = \vec{x}$
$C^0$ across elements, $C^1$ within elements

Generalized Barycentric Coordinates

~~Piecewise linear functions~~
Interpolate nodal data: $\varphi_i\of{\vec{x}_j} = \delta_{ij}$
Partition of unity: $\sum_i \varphi_i\of{\vec{x}} = 1$
Barycentric property: $\sum_i \varphi_i\of{\vec{x}} \vec{x}_i = \vec{x}$
$C^0$ across elements, $C^1$ within elements

Generalized Barycentric Coordinates

Wachspress Coordinates
- Wachspress, Warren
Mean Value Coordinates
- Floater, Hormann, Ju, Wicke
Maximum Entropy Coordinates
- Sukumar, Hormann
Harmonic Coordinates
- Joshi, Martin

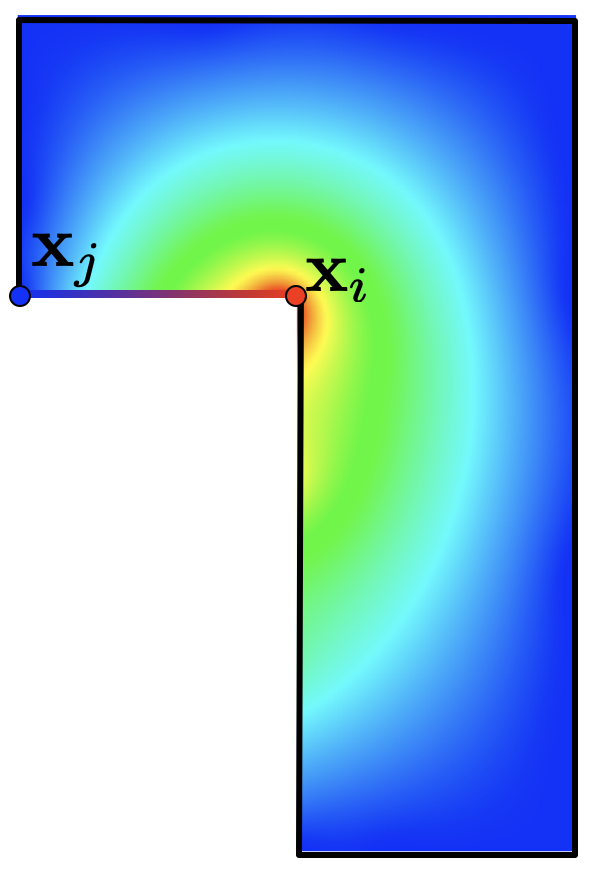
Harmonic Coordinates

Definition
- Interpolate nodal data: $\varphi_i(\vec{x}_j) = \delta_{ij}$
- Linear (=harmonic) on edges
- Harmonic in interior: $\laplace\varphi_i = 0$
Computation
- Method of fundamental solutions
- Approximate shape functions $\varphi_i$ by RBFs $\psi_k$ \[\varphi_i(\vec{x}) = \sum_k w_k \, \psi_k\of{\vec{x}} + \pi_1\of{\vec{x}}\]

Quiz

For which property is the polynomial term $\pi_1\of{\vec{x}}$ crucial? \[\varphi_i(\vec{x}) = \sum_k w_k \, \psi_k\of{\vec{x}} + \pi_1\of{\vec{x}}\]

Laplace Matrix & Mass Matrix

\[ \small \begin{eqnarray*} \mat{L}_{ij} &=& -\int \grad \varphi_i \cdot \grad \varphi_j &=& \color{red}{\xcancel{ \begin{cases} \frac{\cot\alpha_{ij}+\cot\beta_{ij}}{2} & \text{if } j\in\set{N}\of{i} \,, \\[0.5em] \displaystyle -\sum_{k\in\set{N}\of{i}} \mat{L}_{ik} & \text{if } j=i \,, \\[0.3em] 0 & \text{otherwise}. \end{cases} }} \\[1em] \mat{M}_{ij} &=& \int \varphi_i \, \varphi_j &=& \color{red}{\xcancel{ \begin{cases} \frac{\abs{t_{ijk}} + \abs{t_{jih}}}{12} & \text{if } j\in\set{N}\of{i}\,, \\[0.5em] \displaystyle \sum_{k\in\set{N}\of{i}} \mat{M}_{ik} & \text{if }j=i \,,\\[0.3em] 0 & \text{otherwise}. \end{cases} }} \end{eqnarray*} \]

On triangles, harmonic coordinates reproduce barycentric coordinates

Demo: Parameterization

Poisson System on 2D Voronoi Meshes

images/voronoi_plane1.png images/voronoi_plane2.png images/voronoi_plane3.png images/voronoi_plane4.png images/voronoi_plane5.png

Poisson System on 2D Voronoi Meshes

13.5053,	28.5194,	58.8386,	119.78,	241.153
Harmonic,	0.00951959,	0.00236579,	0.000699382,	0.000188646,	5.46139E-05
<!--
{
  "options": {
    "scales": {
      "x": {
        "title": {
          "text": "inverse mean edge length",
          "display": true
        },
        "type": "logarithmic"
      },
      "y": { 
        "title": {
          "text": "L2 error",
          "display": true
        },
        "type": "logarithmic"
      }
    }
  }
}
-->

Expected convergence rate 😄 Expensive to compute, evaluate, and integrate 😢

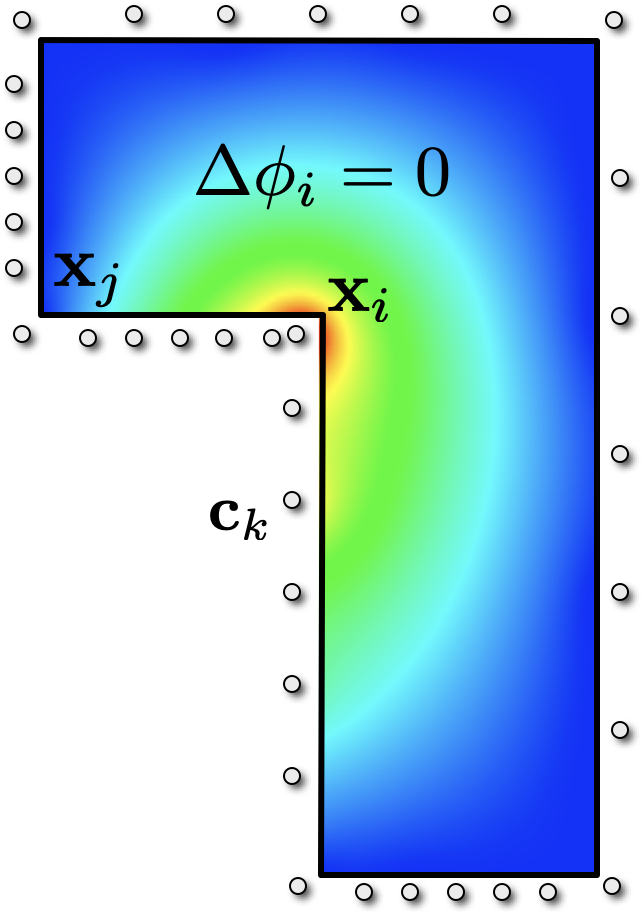
Harmonic Coordinates on Polyhedral Meshes

Approximate 3D shape functions $\varphi_i$ with RBFs $\psi_k$, just as before \[\varphi_i(\vec{x}) = \sum_k w_k \, \psi_k\of{\vec{x}} + \pi_1\of{\vec{x}}\]
Changes:
- Approximate 2D shape functions for each of the polyhedron’s faces
- Sample harmonic Dirichlet boundary conditions with 2D basis
- Change RBFs $\psi_k$ to fundamental solution of 3D Laplace equation

Harmonic Finite Elements

Outline

Introduction
Laplacian for Triangle Meshes
Laplacian for Polygon Meshes
- Martin et al., Polyhedral finite elements using harmonic basis functions, SGP 2008
- Alexa & Wardetzky, Discrete Laplacians on general polygonal meshes, SIG 2011
- de Goes et al., Discrete differential operators on polygonal meshes, SIG 2020
- Bunge et al., Polygon Laplacian made simple, EG 2020
- Bunge et al., The Diamond Laplace for polygonal and polyhedral meshes, SGP 2021
- Bunge et al., Variational quadratic shape functions for polygons and polyhedra, SIG 2022
Comparisons & Conclusion

DEC Polygon Laplacians

Generalize DEC to non-planar polygons
- (Alexa and Wardetzky 2011)
- (deGoes, Butts, and Desbrun 2020)

Discretization of $\laplace f = \delta d f$ (Laplace-de Rham)
- The exterior derivative $d$ becomes the difference operator $\mat{d}$
- The co-differential $\delta$ can be discretized as $\mat{M}_0^{-1} \mat{d}\T \mat{M}_1$
- Putting it together: $\laplace \vec{u} \;\approx\; -\mat{M}_0^{-1} \mat{d}\T \mat{M}_1 \mat{d}\, \vec{u}$

Difference operator

The difference operator maps

Difference operator

The difference operator maps
- From values on vertices (0-forms)

Difference operator

The difference operator maps
- From values on vertices (0-forms)
- To differece values on (half-)edhes (1-forms)

Difference operator

The difference operator maps
- From values on vertices (0-forms)
- To differece values on (half-)edhes (1-forms)

Construction for face $f$ with $n_f$ vertices/edges \[\mat{d}_f = \begin{pmatrix} 1 & 0 & 0 & \cdots & 0 & -1\\ -1 & 1 & 0 & \cdots & 0 & 0\\ 0 & -1 & 1 & \cdots & 0 & 0\\ & & & \vdots \\ 0 & 0 & 0 & \dots & -1 & 1\end{pmatrix}\in \R^{n_f \times n_f}\]
Note that $\mat{d}$ is rectangular, mapping from all vertices to all halfedges

Properties of DEC Laplacian

$\laplace \vec{u} \;\approx\; -\mat{M}_0^{-1} \underbrace{\mat{d}\T \mat{M}_1 \mat{d}}_{-\mat{L}} \, \vec{u}$

The weak Laplacian $\mat{L}$ appears as $-\mat{d}\T \mat{M}_1 \mat{d}$
- Constants are in kernel of $\mat{L}$ because $\mat{d}$ annihilates them 👍
- If $\mat{M}_1$ is symmetric then $\mat{L}$ is symmetric 👍
- If $\mat{M}_1$ is $regular$ then only the constants are in the kernel 👍
Linear precision of $\mat{L}$?
- Strategy: construction per face as $\mat{M}_f$
- Require that $\mat{L}_f = \mat{d}_f\T \mat{M}_f \mat{d}_f$ yields the area gradient as $\left(\mat{L}_f\mat{X}_f\right)_i$ for vertex $i$ 👍
Problem: linear precision + $\mat{M}_f$ regular
- Solved by regularization that introduces a parameter that affects the results 👎

Strategy I: The algebraic approach

Inner Product Matrix

$\mat{B}_f = (\vec{b}_1,\dots,\vec{b}_{n_f})^{\mathsf{T}} \in \R^{n_f \times 3}$
- Rows are barycenters $\vec{b}_i = \frac{1}{2}\left(\mat{x}_{i+1}+\vec{x}_i\right)$ of each edge $\vec{e}_i$.
$|f| $ is vector area of polygon $f$
Define local inner product matrix for 1-forms \[\mat{\tilde{M}}_f = \frac{1}{|f|}\mat{B}_f \mat{B}_f ^{\mathsf{T}}\]
- Not intuitive / easy to see, but not difficult to prove: \[ \grad_{\vec{x}_i}\abs{f} = \left(\tilde{\mat{L}}_f \mat{X}_f\right)_i \]
- Where $\tilde{\mat{L}}_f = \mat{d}_f \mat{\tilde{M}}_f \mat{d}$

Quiz

While $\mat{\tilde{M}}_f = \frac{1}{|f|}\mat{B}_f \mat{B}_f ^{\mathsf{T}}$ is symmetric PSD by construction it may have a kernel.

Which property is lost for $-\mat{L}$ when $\mat{M}_f$ is only semi-definite?

Fill up the Kernel

$\mat{E}_f = (\vec{e}_1,\dots,\vec{e}_{n_f})^{\mathsf{T}} \in \R^{n_f \times 3}$
- Rows are edge vectors of polygon $f$.
$\mathbf{E}_f\T$ has maximal rank 3

$\mat{E}_{\bar{f}} = (\bar{\vec{e}}_1,\dots,\bar{\vec{e}}_{n_f})^{\mathsf{T}} \in \R^{n_f \times 3}$
- Rows are edge vectors of maximal projection $\bar{f}$.
$\mat{E}\T_{\bar{f}}$ has rank 2 $\rightarrow$ non-trivial kernel

Regularizer

Add regularizer matrix $\mat{R}_f$ to fill up kernel \[\mat{M}_{f} = \mat{\tilde{M}}_f + \lambda\mat{R}_f\]
- Built from orthonormal kernel $\mat{K}_{\bar{f}}\T$ of $\mat{E}_{\bar{f}}^{\mathsf{T}}$
- Suggestion: $\mat{R}_f = \mat{K}_{\bar{f}} \mat{I} \mat{K}_{\bar{f}}\T$
- Identity $\mat{I}$ could be replaced with any symmetric PD matrix

Laplace and Mass Matrices

Local Laplace matrix per polygon \[ {\mat{L}}_f = \mat{d}\T \mat{M}_{f} \mat{d} \]
- Assemble local matrices into global Laplace matrix $\mat{L}$
Global mass matrix $\mat{M}$ with
\[\mat{M}_{ii} = \sum_{f \ni v_i} \frac{|\bar{f}|}{n_f}\]

Poisson System on 2D Voronoi Meshes

13.5053,	28.5194,	58.8386,	119.78,	241.153
Alexa11; λ=2,	0.00838748,	0.00209687,	0.000476346,	0.000127937,	3.30444E-05
Alexa11; λ=1,	0.00456036,	0.0010483,	0.000382806,	8.53325E-05,	1.84683E-05
Alexa11; λ=0.5,	0.00800984,	0.00193734,	0.000621653,	0.000143936,	3.19937E-05
Alexa11; λ=0.1,	0.0144414,	0.00337097,	0.000947331,	0.000221091,	5.14271E-05
<!--
{
  "options": {
    "scales": {
      "x": {
        "title": {
          "text": "inverse mean edge length",
          "display": true
        },
        "type": "logarithmic"
      },
      "y": { 
        "title": {
          "text": "L2 error",
          "display": true
        },
        "type": "logarithmic"
      }
    }
  }
}
-->

Strategy II: Stokes’ Theorem on Cogradient

Quiz

Which part of the integrals causes problems for non-planar polygons? \[\iint_f \grad u(\vec{x}) \d{A} = \oint_{\partial f} u(\vec{x}) \vec{t}(\vec{x}) \times \vec{n}(\vec{x}) \d{\vec{x}} \]

Tangent vector $\vec{t}(\vec{x})$ at point $\vec{x}$
Surface normal $\vec{n}(\vec{x})$ at point $\vec{x}$
The integral over the boundary of the polygon
The function values $u(\vec{x})$ at the boundary of the polygon

Cogradient

Cogradient operator \[\grad u^{\bot}(\vec{x}) := \vec{n}(\vec{x}) \times \grad u(\vec{x}),\]
- Gradient of $u(\vec{x})$ locally rotated by 90 degrees around normal $\vec{n}(\vec{x})$
Use Stoke’s theorem \[\iint_f \grad u^{\bot}(\vec{x}) \d{A} = \oint_{\partial f} u(\vec{x}) \vec{t}(\vec{x}) \d{\vec{x}}\]
- $\vec{t}(\vec{x})$ is unit tangent vector at boundary point $\vec{x}$
- Well-defined along polygon boundary

Integrated Cogradient

Consider linear functions $u$!
- For linear functions the gradient is constant: \[\iint_f \grad u^{\bot}(\vec{x}) \d{A} = \iint_f \vec{n}(\vec{x}) \times \grad u(\vec{x}) \d{A} = \left(\iint_f \vec{n}(\vec{x}) \d{A}\right) \times \grad u(\vec{x})\]
- Integrated normal $\vec{n}(\vec{x})$ is the area vector $\vec{a}_f$
  - Independent of spanning surface
  - Can be computed from boundary (polygon)
- The contour integral becomes a sum over edge vectors times average values on edges: \[\oint_{\partial f} u(\vec{x}) \vec{t}(\vec{x}) \d{\vec{x}} = \mat{E}_f\T\mat{A}_f\]
Gives expression for polygon gradient operator $\vec{G}_f = -\|\vec{a}_f\|^{-2}\vec{a}_f \times \mat{E}_f\T\mat{A}_f$

Musical Operators

Construction of Laplace operator from gradient leads to non-trivial kernel
- Similar to previous construction
More careful construction using musical operators
- Flat $(\flat)$ operator transforms vector to 1-form
- Sharp $(\sharp)$ operator transforms 1-form to vector
Sharp operator defines gradient in smooth setting $\grad u = (\d u)^{\sharp}$
Discrete version: $\mat{G}_f = \mat{V}_f^{\sharp}\mat{d}_f$
- $\mat{V}_f^{\sharp}$ maps
  - From 1-form (difference values at edges)
  - To vector in the polygon plane (tangent vector)
- Use $\mat{G}_f$ to construct $\mat{V}_f^{\sharp}$

First Attempt for Inner Product Matrix

\[\mat{\tilde{M}}_f = \abs{\bar{f}} \, \mat{V}_f^{\sharp \mathsf{T}} \, \mat{V}_f^{\sharp}\]

$\mat{\tilde{M}}_f$ is a dot product of tangent vectors
Mapping $n_f$ values to tangent vector leads to loss of information 😢
- Add regularizer for kernel dimension 👍

Regularizer

Add regularizer matrix $\mat{R}_f$ to fill up kernel \[\mat{M}_{f} = \mat{\tilde{M}}_f + \lambda\mat{R}_f\]
- Construct flat operator $\mat{V}_f^{\flat}$
  - Use that $\mat{V}_f^{\sharp}\mat{V}_f^{\flat}$ preserves tangent vectors
- Projection $\mat{P}_f = \mat{I} - \mat{V}_f^{\flat}\mat{V}_f^{\sharp}$ encodes loss from projecting to tangent vectors
- Regularizer $\mat{R}_f = \mat{P}_f\T\mat{P}_f$ spans the non-trivial kernel

Laplace and Mass Matrices

Local Laplace matrix per polygon \[ {\mat{L}}_f = \mat{d}\T \mat{M}_f\mat{d} \]
- Assemble into global matrix $\mat{L}$
Global mass matrix $\mat{M}$ same as Alexa and Wardetzky

Poisson System on 2D Voronoi Meshes

13.5053,	28.5194,	58.8386,	119.78,	241.153
deGoes20; λ=2,	  0.00965471,	0.00245388,	  0.000542276,	0.000145297,	3.74297E-05
deGoes20; λ=1,	  0.00435302,	0.000996788,	0.000354402,	7.95537E-05,	1.73643E-05
deGoes20; λ=0.5,	0.00747841,	0.00182759,	  0.00059557,	  0.000138136,	3.05869E-05
deGoes20; λ=0.1,	0.0139834,	0.00327528,	  0.00092799,	  0.000217473,	5.03785E-05
<!--
{
  "options": {
    "scales": {
      "x": {
        "title": {
          "text": "inverse mean edge length",
          "display": true
        },
        "type": "logarithmic"
      },
      "y": { 
        "title": {
          "text": "L2 error",
          "display": true
        },
        "type": "logarithmic"
      }
    }
  }
}
-->

Demo: Curvature

Outline

Introduction
Laplacian for Triangle Meshes
Laplacian for Polygon Meshes
- Martin et al., Polyhedral finite elements using harmonic basis functions, SGP 2008
- Alexa & Wardetzky, Discrete Laplacians on general polygonal meshes, SIG 2011
- de Goes et al., Discrete differential operators on polygonal meshes, SIG 2020
- Bunge et al., Polygon Laplacian made simple, EG 2020
- Bunge et al., The Diamond Laplace for polygonal and polyhedral meshes, SGP 2021
- Bunge et al., Variational quadratic shape functions for polygons and polyhedra, SIG 2022
Comparisons & Conclusion

Prolongation Operator

images/poly11.svg \[ {\Huge \downarrow} \; \mat{P} \] images/poly31.svg

Insert virtual vertex as affine combination \[ \small \matrix{ \sum_i w_i \vec{x}_{i}\\ \vec{x}_{1}\\ \vec{x}_{2}\\ \vec{x}_{3}\\ \vec{x}_{4}\\ \vec{x}_{5}\\ \vec{x}_{6} } = \underbrace{ \matrix{ w_1 & w_2 & w_3 & w_4 & w_5 & w_6\\ 1 & & & & & \\ & 1 & & & & \\ & & 1 & & & \\ & & & 1 & & \\ & & & & 1 & \\ & & & & & 1 } }_{\mat{P}} \matrix{ \vec{x}_{1}\\ \vec{x}_{2}\\ \vec{x}_{3}\\ \vec{x}_{4}\\ \vec{x}_{5}\\ \vec{x}_{6} } \]

Restriction Operator

images/poly11.svg \[ {\Huge \uparrow} \; \mat{R} = \mat{P}\T \] images/poly41.svg

Redistribute values back to original nodes \[ \mat{R} = \mat{P}\T \]

Polygon Shape Functions

images/poly11.svg \[\downarrow\] images/poly31.svg \[\downarrow\] images/poly41.svg

Insert center vertex through prolongation weights
Compute standard linear shape functions $\psi_j(\vec{x})$ on refined polygon
Coarse shape function for polygon $(\vec{x}_1, \dots, \vec{x}_n)$ with virtual vertex $\vec{x}_0$ become \[ \varphi_i(\vec{x}) = \psi_i(\vec{x}) + w_i\psi_0(\vec{x}) \,,\quad i \in \{1, \dots, n\} \]

Polygon Shape Functions

Piecewise linear functions
Interpolate nodal data: $\varphi_i\of{\vec{x}_j} = \delta_{ij}$
Partition of unity: $\sum_i \varphi_i\of{\vec{x}} = 1$
Barycentric property: $\sum_i \varphi_i\of{\vec{x}} \vec{x}_i = \vec{x}$
$C^0$ across elements, not $C^1$ within elements

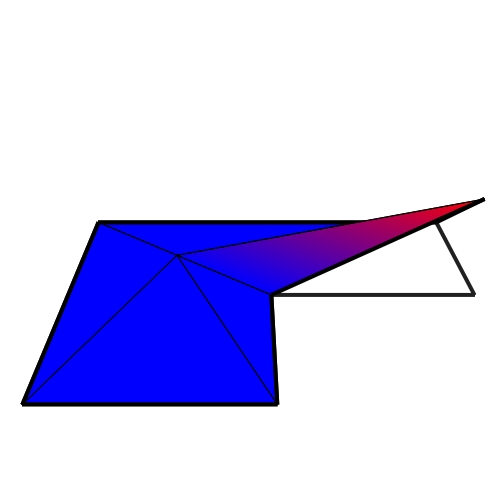
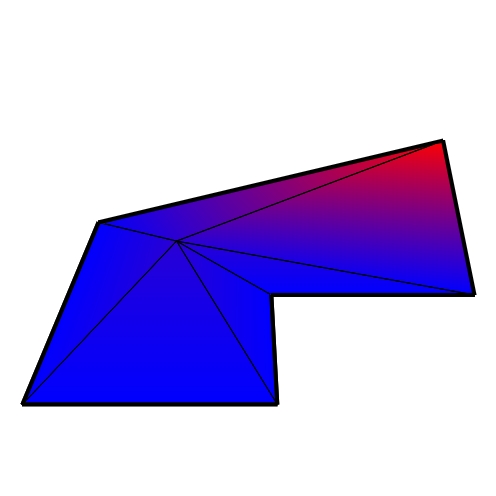
images/basis/L.0.jpg images/basis/L.1.jpg images/basis/L.2.jpg images/basis/L.3.jpg images/basis/L.4.jpg images/basis/L.5.jpg

Choice of Virtual Vertex

images/quadratic_good.svg — Minimize sum of squared areas

Solve linear system for affine prolongation weights 👍

Quiz

For which (planar) elements would the virtual vertex lead to flipped virtual triangles?

Star-shaped elements
Convex elements
Non-star-shaped elements
Concave elements

Laplace Matrix & Mass Matrix

“Sandwiched” Laplace matrix for polygons \[\mat{L} = \mat{P}\T \, \mat{L}^\func{tri} \, \mat{P} \]
“Sandwiched” mass matrix for polygons \[\mat{M} = \mat{P}\T \, \mat{M}^\func{tri} \, \mat{P} \]
Laplacian can be factored into divergence and gradient \[ \mat{L} = \underbrace{\mat{P}\T \mat{D}^\func{tri}}_{\mat{D}} \cdot \underbrace{\mat{G}^\func{tri} \mat{P}}_{\mat{G}} \]

Virtual refinement is completely hidden in matrix assembly step!

Demo: Smoothing

Poisson System on 2D Voronoi Meshes

13.5053,	28.5194,	58.8386,	119.78,	241.153
Bunge20, 0.00768401,0.00193955,0.00057802,0.000152567,3.41754E-05

<!--
{
  "options": {
    "scales": {
      "x": {
        "title": {
          "text": "inverse mean edge length",
          "display": true
        },
        "type": "logarithmic"
      },
      "y": { 
        "title": {
          "text": "L2 error",
          "display": true
        },
        "type": "logarithmic"
      }
    }
  }
}
-->

Linear Shape Functions for Polyhedra

images/cube.png images/cubef.png images/cubefc.png

Insert virtual face point
- Minimizer of squared triangle areas
Insert virtual cell point
- Minimizer of squared tetrahedra volumes
Two-step prolongation \[ \mathbf{P} = \mat{P}_c \, \mat{P}_f\]

Outline

Introduction
Laplacian for Triangle Meshes
Laplacian for Polygon Meshes
- Martin et al., Polyhedral finite elements using harmonic basis functions, SGP 2008
- Alexa & Wardetzky, Discrete Laplacians on general polygonal meshes, SIG 2011
- de Goes et al., Discrete differential operators on polygonal meshes, SIG 2020
- Bunge et al., Polygon Laplacian made simple, EG 2020
- Bunge et al., The Diamond Laplace for polygonal and polyhedral meshes, SGP 2021
- Bunge et al., Variational quadratic shape functions for polygons and polyhedra, SIG 2022
Comparisons & Conclusion

Finite Volumes

Main idea: Consider the integral of differential in a small region

Divergence: \[\iint_{\Omega} \text{div} \vec{u}\ \d{A} = \oint_{\partial \Omega} \vec{u}\tp\vec{n} \d{s}\]
Gradient: \[\iint_\Omega \nabla u \d{A} = \oint_{\partial \Omega} u\, \mat{n} \d{s}\]
Laplacian: \[\iint_\Omega \Delta u \d{A} = \oint_{\partial \Omega} \nabla u\tp \mat{n} \d{s}\]

Discrete Duality Finite Volumes (DDFV)

images/mesh.svg images/dual_mesh.svg images/dual_controlvolume.svg images/primal_controlvolume.svg images/dual_mesh_diamond.svg images/diamond_mesh.svg

Quiz

How do we get diamond cells on an arbitrary polygon mesh?

Subdivide into triangles
Subdivide into quads
Connect primal and dual vertices
Introduce third control mesh

images/poly_mesh_dual.svg images/poly_mesh_diamond.svg

2D DDFV

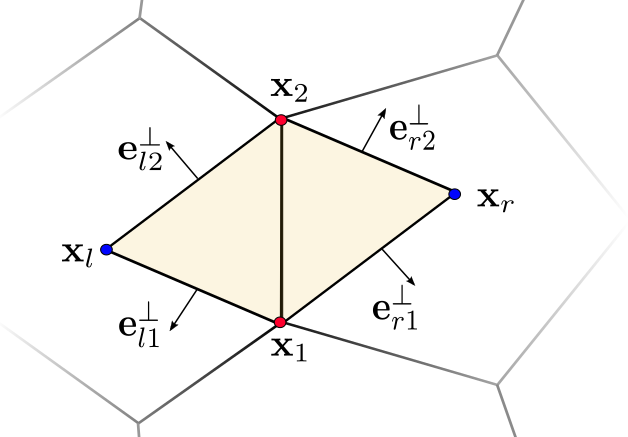
\[ \grad u|_D \;=\; \frac{1}{2 \abs{D}} \sum_{(i,j) \in \partial D} \vec{e}_{ij}^\perp \frac{u_i+u_j}{2} \]

Limitations of DDFV

Typically only primal mesh is given
Dual vertices increase DoF significantly
Only defined on 2D planar meshes, not on two-manifolds

Virtual Dual Vertices

images/poly11.svg \[\downarrow\] images/poly31.svg \[\downarrow\] images/poly41.svg

Combine ideas from DDFV and virtual refinement
Use virtual vertices as dual mesh
Compute DDFV operator on the “virtual diamonds”
- Express diamond in an intrinsic 2D coordinate system
Restrict values back to the original mesh

Limitations of DDFV

Typically only primal mesh is given
Dual vertices increase DoF significantly
Only defined on 2D planar meshes, not on two-manifolds

Diamond Gradient Operator

The $i$-th column of the diamonds gradient matrix $\mat{G}_D \in \R^{2 \times 4}$ \[ \mat{G}_D(:,i) = \frac{1}{2 \abs{D}} \sum_{(i,j) \in \partial D} \vec{e}_{ij}^\perp \]
Mesh gradient $\hat{\mat{G}}$ is combined with prolongation $\mat{P}$ to form global operator \[ \mat{G} = \hat{\mat{G}} \, \mat{P} \,\in\R^{2\abs{\mathcal{E}} \times \abs{\mathcal{V}}} \]

Diamond Divergence Operator

The diamond divergence matrix is defined as \[ \mat{D} = -\mat{P}\tp \hat{\mat{G}}\tp \hat{\mat{M}}_\diamond \]
$\hat{\mat{M}}_\diamond$ is diagonal matrix of diamond areas

Laplace Operator

Laplacian matrix is defined as \[ \mat{L} \;=\; \underbrace{-\mat{P}\tp \hat{\mat{G}}\tp \hat{\mat{M}}_\diamond}_{\mat{D}} \cdot \underbrace{\hat{\mat{G}} \mat{P}}_{\mat{G}} \]
Mass matrix derived from standard DDFV mass matrix $\mat{M}_\diamond$ \[ \mat{M} \;=\; \mat{P}\tp \mat{M}_\diamond \mat{P} \]

Demo: Geodesics

Properties

Poisson System on 2D Voronoi Meshes

13.5053,	28.5194,	58.8386,	119.78,	241.153
Diamond, 0.00610683,0.00155889,0.000413685,0.000105977,2.46064E-05
<!--
{
  "options": {
    "scales": {
      "x": {
        "title": {
          "text": "inverse mean edge length",
          "display": true
        },
        "type": "logarithmic"
      },
      "y": { 
        "title": {
          "text": "L2 error",
          "display": true
        },
        "type": "logarithmic"
      }
    }
  }
}
-->

Diamond Laplace on Polyhedral Meshes

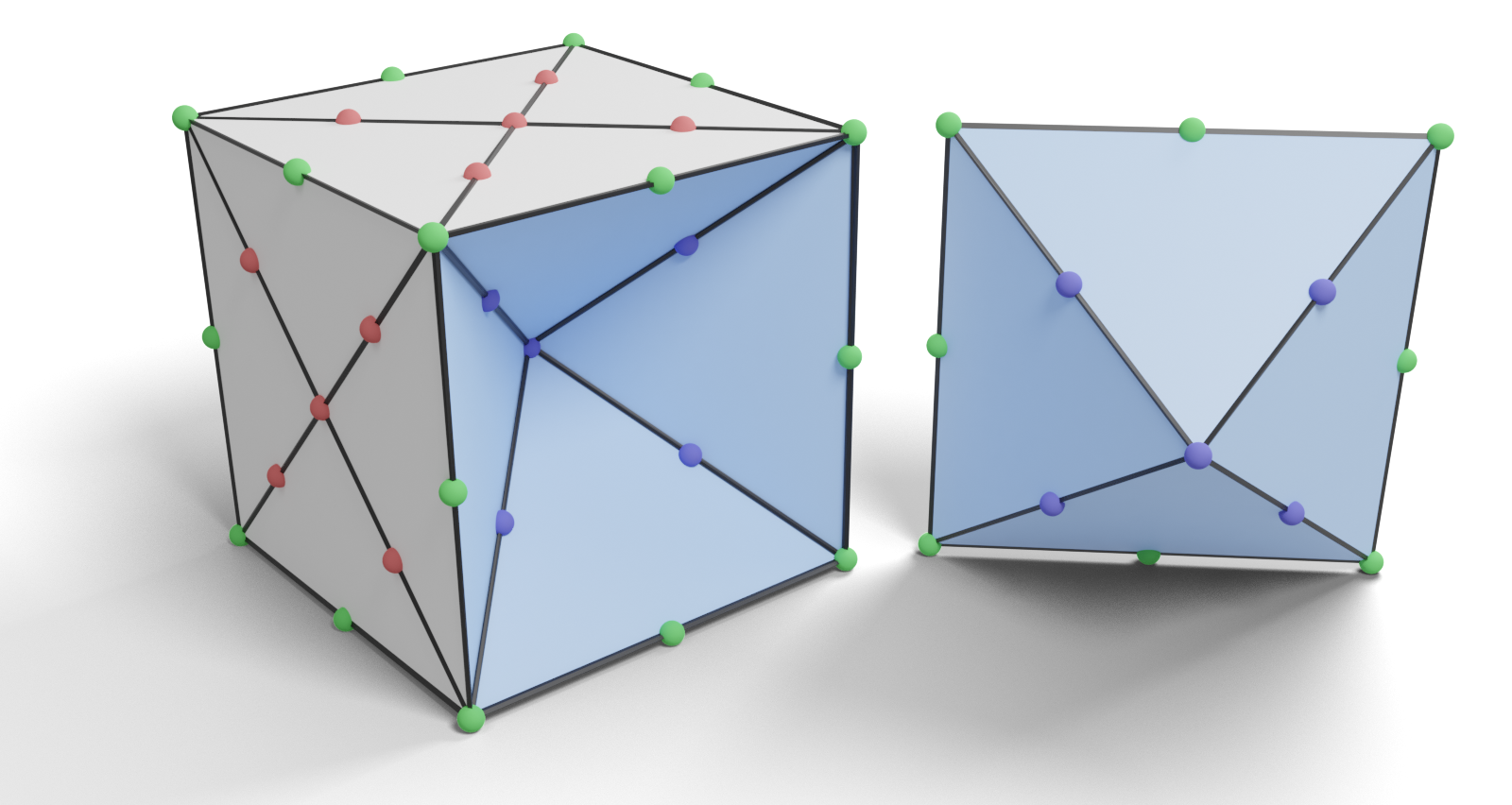
Same two-step prolongation as linear virtual refinement method \[ \mathbf{P} = \mat{P}_c \, \mat{P}_f\]
Construct minimal diamond cells

Volume Diamond Gradient

\[\begin{equation*} \grad u|_\Omega = \frac{1}{3\abs{\Omega}} \sum_{(i,j,k) \in \partial \Omega} \vec{a}_{ijk} \left( u_i+u_j+u_k \right) \end{equation*}\]

\[\begin{equation*} \mat{G}_\Omega(:,i) = \frac{1}{3 \abs{\Omega}} \sum_{(i,j,k) \in \partial \Omega} \vec{a}_{ijk}, \end{equation*}\]

Outline

Introduction
Laplacian for Triangle Meshes
Laplacian for Polygon Meshes
- Martin et al., Polyhedral finite elements using harmonic basis functions, SGP 2008
- Alexa & Wardetzky, Discrete Laplacians on general polygonal meshes, SIG 2011
- de Goes et al., Discrete differential operators on polygonal meshes, SIG 2020
- Bunge et al., Polygon Laplacian made simple, EG 2020
- Bunge et al., The Diamond Laplace for polygonal and polyhedral meshes, SGP 2021
- Bunge et al., Variational quadratic shape functions for polygons and polyhedra, SIG 2022
Comparisons & Conclusion

Linear Elasticity

Locking due to high Poisson ratio 😢

Linear vs Quadratic

images/linear2.svg — Linear Lagrange Elements

images/quad2.svg — Quadratic Lagrange Elements

Quiz

Given a quad, how many virtual degrees of freedom do we need for the quadratic Lagrange elements?

Four virtual vertices
Five virtual vertices
Twelve virtual vertices
Thirteen virtual vertices

Quiz

Given a quad, how many virtual degrees of freedom do we need for the quadratic Lagrange elements?

Quadratic Polygon Shape Functions

Compute standard quadratic shape functions $\psi_j(\vec{x})$ on refined polygon
Shape functions for polygon $(\vec{x}_1, \dots, \vec{x}_n)$ with coarse DoFs $\mathcal{C}$ and virtual DoFs $\mathcal{K}$ \[ {\color{green}\varphi_i(\vec{x})} = {\color{green}\psi_i(\vec{x})} + \sum_{j\in \mathcal K} w_{ij} {\color{red} \psi_j(\vec{x})} \quad\text{ for } i \in \mathcal C. \]

Prolongation Weights Influence Convergence

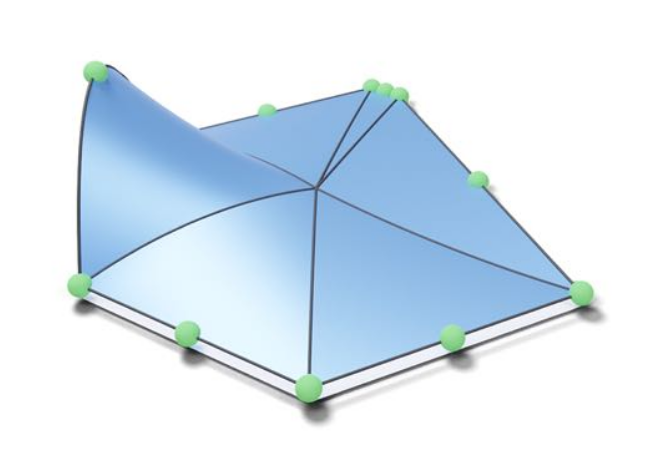
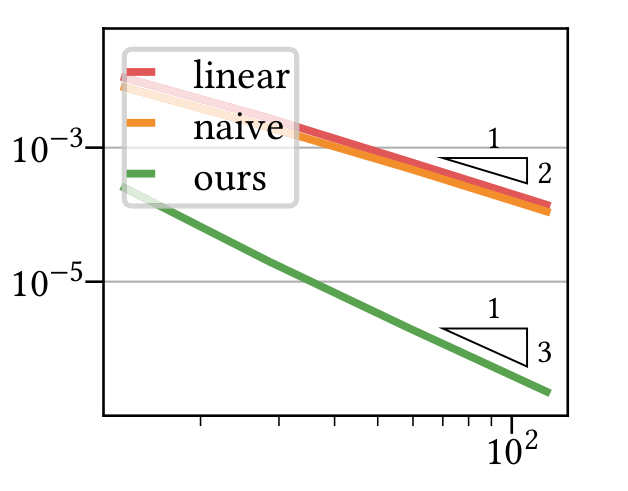
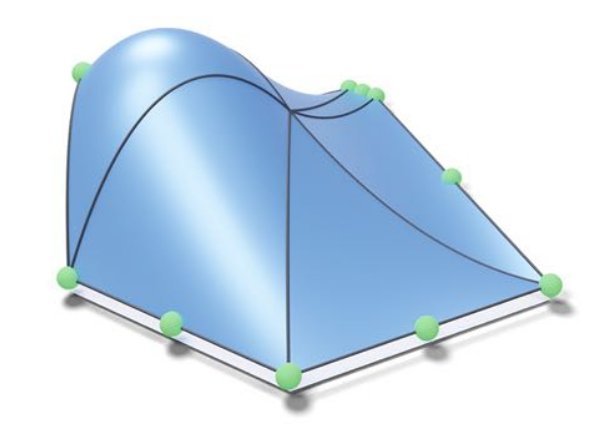
Optimize for Smoothness

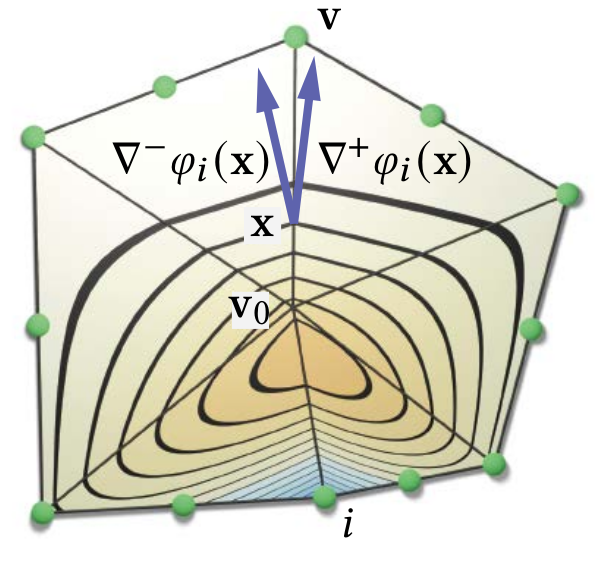
Shape functions for polygon $(\vec{x}_1, \dots, \vec{x}_n)$ \[ {\color{green}\varphi_i(\vec{x})} = {\color{green}\psi_i(\vec{x})} + \sum_{j\in \mathcal K} w_{ij} {\color{red} \psi_j(\vec{x})} \quad\text{ for } i \in \mathcal C. \]
Solve variational optimization per cell \[ \min_{\{w_{ij}\}} \sum_{i \in \mathcal C} \sum_{\sigma \in \mathcal E^*} \int_\sigma \norm{ \nabla_\sigma^+ \varphi_i - \nabla_\sigma^- \varphi_i }^2 \ \mathrm{d}\sigma \]
Only needs a linear system solve 👍

Properties of Shape Functions

Reproduce $P2$ on triangle meshes (proven)
Lagrange interpolation property (by construction)
Partition of unity (hard constraint)
Linear precision (hard constraint)
Quadratic precision (empirical observation)

Linear Elasticity

images/quad_elasticity.png — quadratic shape functions

Geodesic Distances

Poisson System on 2D Voronoi Meshes

13.5053,	28.5194,	58.8386,	119.78,	241.153
Quadratic Virtual Refinement,  0.000249856,1.9939E-05,2.01787E-06,2.2815E-07,2.72628E-08
<!--
{
  "options": {
    "scales": {
      "x": {
        "title": {
          "text": "inverse mean edge length",
          "display": true
        },
        "type": "logarithmic"
      },
      "y": { 
        "title": {
          "text": "L2 error",
          "display": true
        },
        "type": "logarithmic"
      }
    }
  }
}
-->

Poisson System on 2D Voronoi Meshes

13.5053,	28.5194,	58.8386,	119.78,	241.153
Harmonic,	       0.00951959,	0.00236579,	0.000699382,	0.000188646,	5.46139E-05
Alexa11; λ=2,	0.00838748,	0.00209687,	0.000476346,	0.000127937,	3.30444E-05
Alexa11; λ=1,	0.00456036,	0.0010483,	0.000382806,	8.53325E-05,	1.84683E-05
Alexa11; λ=0.5,	0.00800984,	0.00193734,	0.000621653,	0.000143936,	3.19937E-05
Alexa11; λ=0.1,	0.0144414,	0.00337097,	0.000947331,	0.000221091,	5.14271E-05
deGoes20; λ=2,	0.00965471,	0.00245388,	0.000542276,	0.000145297,	3.74297E-05
deGoes20; λ=1,	0.00435302,	0.000996788,	0.000354402,	7.95537E-05,	1.73643E-05
deGoes20; λ=0.5,0.00747841,	0.00182759,	0.00059557,	0.000138136,	3.05869E-05
deGoes20; λ=0.1,0.0139834,	0.00327528,	0.00092799,	0.000217473,	5.03785E-05
Linear Virtual Refinement,	      0.00768401,	0.00193955,	0.00057802,	0.000152567,	3.41754E-05
Diamond,        0.00610683,0.00155889,0.000413685,0.000105977,2.46064E-05
Quadratic Virtual Refinement,        0.000249856,1.9939E-05,2.01787E-06,2.2815E-07,2.72628E-08
<!--
{
  "options": {
    "scales": {
      "x": {
        "title": {
          "text": "inverse mean edge length",
          "display": true
        },
        "type": "logarithmic"
      },
      "y": { 
        "title": {
          "text": "L2 error",
          "display": true
        },
        "type": "logarithmic"
      }
    }
  }
}
-->

Quadratic Shape Functions for Polyhedra

\[ \small \min_{\{w_{ij}\}} \sum_{i \in \mathcal C} \sum_{\sigma \in \mathcal T^*} \int_\sigma \norm{\nabla_\sigma^+ \varphi_i - \nabla_\sigma^- \varphi_i}^2 \mathrm{d}\sigma \]

Quadratic Shape Functions for Polyhedra

Linear Elasticity

Outline

Introduction
Laplacian for Triangle Meshes
Laplacian for Polygon Meshes
- Martin et al., Polyhedral finite elements using harmonic basis functions, SGP 2008
- Alexa & Wardetzky, Discrete Laplacians on general polygonal meshes, SIG 2011
- de Goes et al., Discrete differential operators on polygonal meshes, SIG 2020
- Bunge et al., Polygon Laplacian made simple, EG 2020
- Bunge et al., The Diamond Laplace for polygonal and polyhedral meshes, SGP 2021
- Bunge et al., Variational quadratic shape functions for polygons and polyhedra, SIG 2022
Comparisons & Conclusion

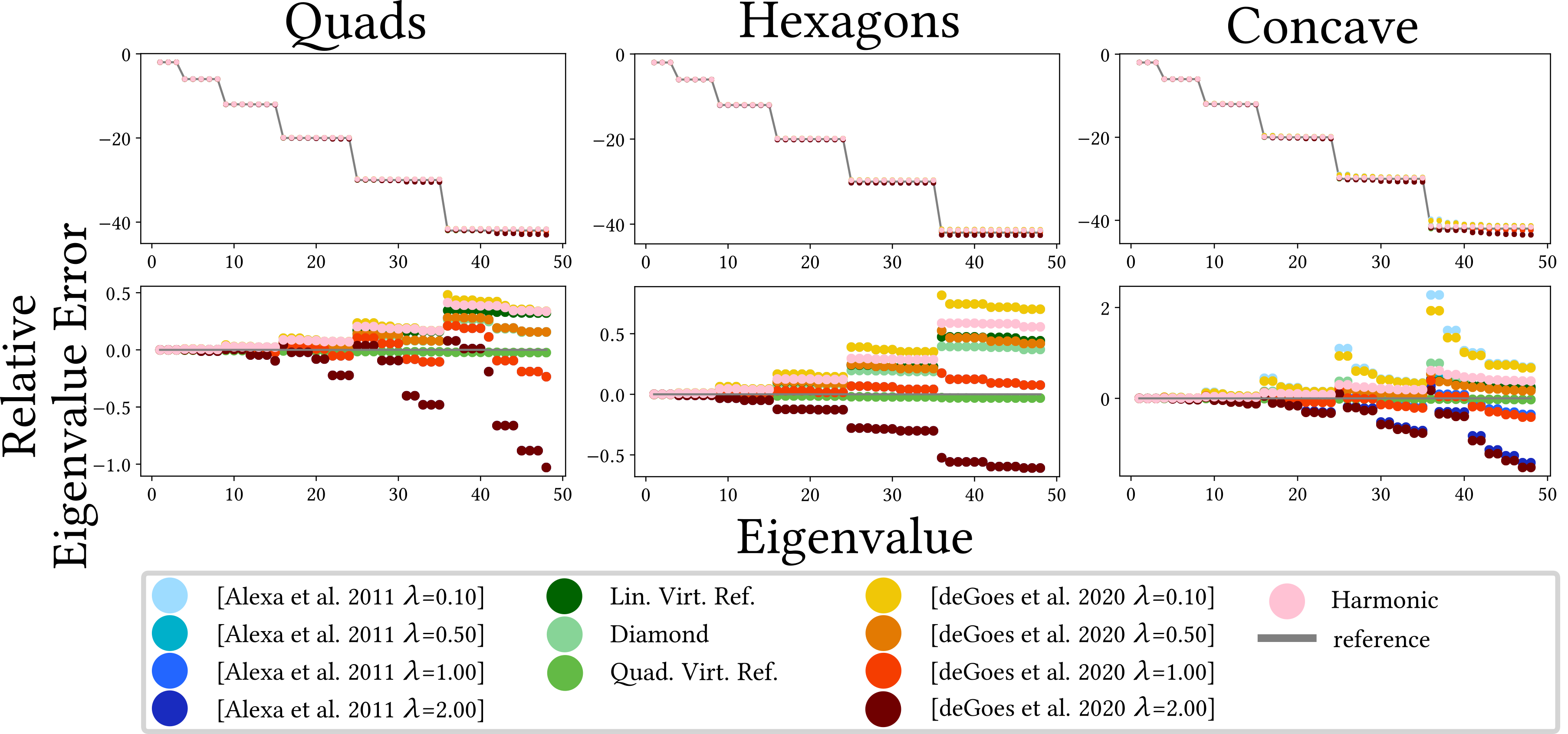
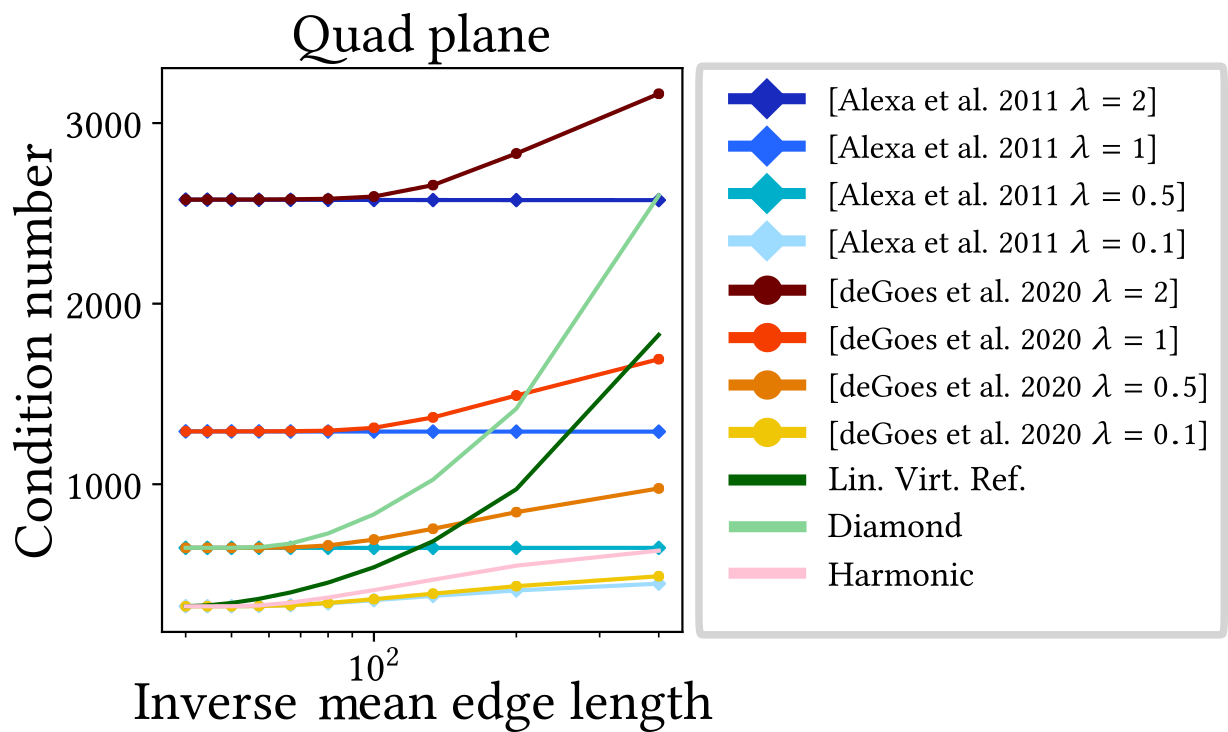
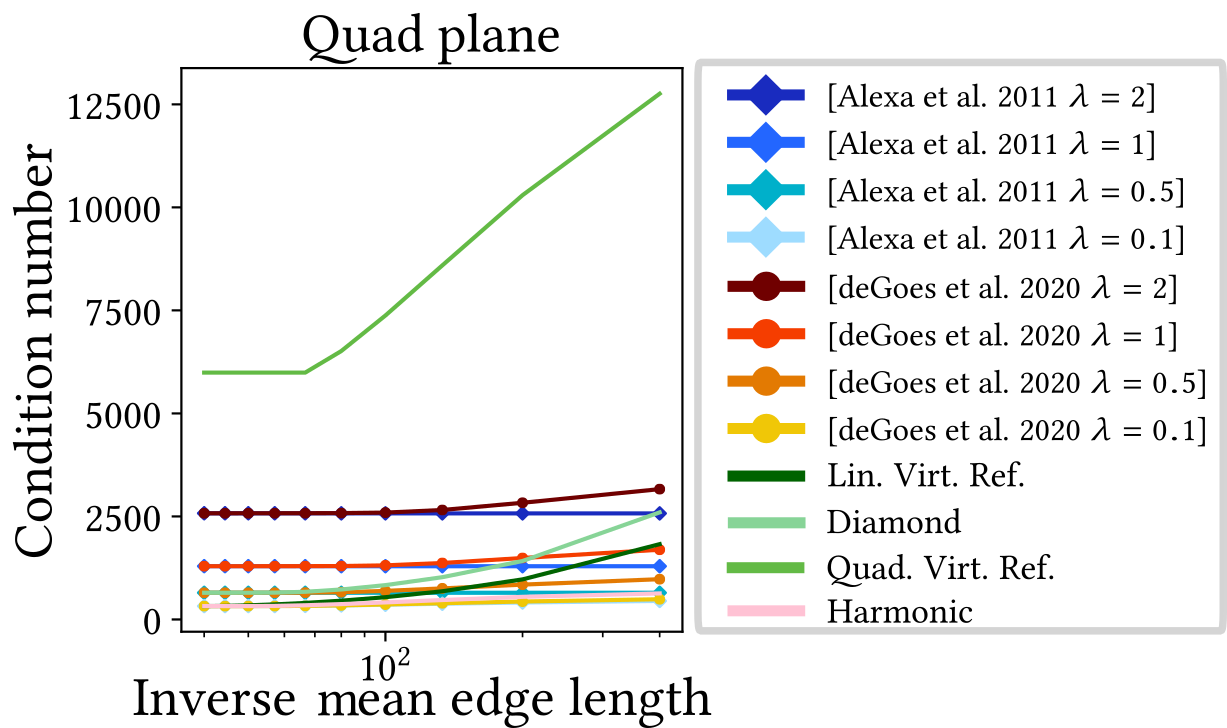
Quantitative Comparisons

Ensure fair comparisons
All methods (re)implemented in C++
Same meshes & test for all methods
Code checked by original authors (Thanks 👍)
Source code for all Laplace operators, quantitative tests, and interactive demos is available on github

Poisson System on 2D Planes

Eigenvalues on Unit Spheres

Condition Number

Condition Number

Computational Performance

code-c0aa2a4b.tex.svg — Time for building and solving a Poisson system

Computational Performance

code-1f19cad7.tex.svg — Time for solving a Poisson system

Conclusion

Presented recent progress for Polygon Laplacians
- Discuss individual discretization strategies
- Point out similarities and differences
- Analyze individual strength and weaknesses
Extensions
- More details on volume meshes (see course notes)

Acknowledgments
- Collaborators: Philipp Herholz, Misha Kazhdan, Olga Sorkine-Hornung
- Code-Checkers: Fernando de Goes, Max Wardetzky

References

Alexa, Marc, and Max Wardetzky. 2011. “Discrete Laplacians on General Polygonal Meshes.” ACM Transactions on Graphics 30 (4).

Brezzi, Franco, Konstantin Lipnikov, and Valeria Simoncini. 2005. “A Family of Mimetic Finite Difference Methods on Polygonal and Polyhedral Meshes.” Mathematical Models and Methods in Applied Sciences 15 (10).

Bunge, Astrid, Mario Botsch, and Marc Alexa. 2021. “The Diamond Laplace for Polygonal and Polyhedral Meshes.” Computer Graphics Forum 40 (5).

Bunge, Astrid, Philipp Herholz, Misha Kazhdan, and Mario Botsch. 2020. “Polygon Laplacian Made Simple.” Computer Graphics Forum 39 (2).

Bunge, Astrid, Philipp Herholz, Olga Sorkine-Hornung, Mario Botsch, and Michael Kazhdan. 2022. “Variational Quadratic Shape Functions for Polygons and Polyhedra.” ACM Transactions on Graphics 41 (4).

deGoes, Fernando, Andrew Butts, and Mathieu Desbrun. 2020. “Discrete Differential Operators on Polygonal Meshes.” ACM Transactions on Graphics 39 (4).

Hermeline, F. 2000. “A Finite Volume Method for the Approximation of Diffusion Operators on Distorted Meshes.” J. Comput. Phys. 160 (2).

Hormann, Kai, and N. Sukumar. 2017. Generalized Barycentric Coordinates in Computer Graphics and Computational Mechanics. Taylor & Francis.

Martin, Sebastian, Peter Kaufmann, Mario Botsch, Martin Wicke, and Markus Gross. 2008. “Polyhedral Finite Elements Using Harmonic Basis Functions.” Computer Graphics Forum 27 (5).

Pinkall, Ulrich, and Konrad Polthier. 1993. “Computing Discrete Minimal Surfaces and Their Conjugates.” Experim. Math. 2.

Wardetzky, Max, Saurabh Mathur, Felix Kälberer, and Eitan Grinspun. 2007. “Discrete Laplace Operators: No Free Lunch.” In Proceedings of Eurographics Symposium on Geometry Processing.

Slides are available online

Problem Setting

Laplacian is a central operator

Diffusion Equation: \(\dot f = \lambda \laplace f\)

Laplace Equation: \(-\laplace f = 0\)

Discrete Laplacian has various applications

Discrete Laplacians for Polygonal/Polyhedral Meshes

Artist-Made Polygon Meshes

Adaptive Refinement

Cutting & Fracturing

Discrete Laplacians for Polygonal Meshes

Triangulate the Polygons?

Outline

Triangle Meshes

Functions on Triangle Meshes

Barycentric Coordinates as Shape Functions

Laplace Matrix & Mass Matrix

Local to Global Assembly

Properties

Quiz

Properties

Poisson System on 2D Triangle Meshes

Poisson System on 2D Triangle Meshes

Poisson System on 2D Triangle Meshes

Outline

Barycentric Coordinates

Generalized Barycentric Coordinates

Generalized Barycentric Coordinates

Harmonic Coordinates

Quiz

Laplace Matrix & Mass Matrix

Demo: Parameterization

Properties

Poisson System on 2D Voronoi Meshes

Poisson System on 2D Voronoi Meshes

Harmonic Coordinates on Polyhedral Meshes

Harmonic Finite Elements

Outline

DEC Polygon Laplacians

Difference operator

Difference operator

Difference operator

Difference operator

Properties of DEC Laplacian

Strategy I: The algebraic approach

Inner Product Matrix

Quiz

Fill up the Kernel

Regularizer

Laplace and Mass Matrices

Properties

Poisson System on 2D Voronoi Meshes

Strategy II: Stokes’ Theorem on Cogradient

Quiz

Cogradient

Integrated Cogradient

Musical Operators

First Attempt for Inner Product Matrix

Regularizer

Laplace and Mass Matrices

Properties

Poisson System on 2D Voronoi Meshes

Demo: Curvature

Outline

Virtual Simplicial Refinement

Prolongation Operator

Restriction Operator

Polygon Shape Functions

Polygon Shape Functions

Choice of Virtual Vertex

Quiz

Laplace Matrix & Mass Matrix

Demo: Smoothing

Properties

Poisson System on 2D Voronoi Meshes

Linear Shape Functions for Polyhedra

Outline

Finite Volumes

Discrete Duality Finite Volumes (DDFV)

Quiz